Machine-Learning Interatomic Potentials

Interatomic Interaction Models

Many research areas in materials science, molecular physics, chemistry, and biology involve atomistic modeling. Atomistic modeling typically uses either empirical interatomic potentials or the quantum-mechanical (QM) models. The models of the first class are very computationally efficient, however, their accuracy is often insufficient to predict the correct behavior of a molecular system. The QM models are more accurate, but computationally expensive. Many practical applications require the accuracy of QM models and the computational efficiency of the empirical models. This project focuses on developing machine-learning interatomic potentials (MLIPs) which are able to reproduce the behavior of any QM model and have the computational efficiency of the empirical models.

We collaborate with materials scientists and chemists on applying our models to:

• materials discovery
• modelling cathodes
• first-principles calculation of alloy phase diagrams
• prediction of chemical reaction rates

How important is this?

Moore’s law suggests that the power of modern supercomputers grows 10 times every 5 years. Yet, molecular modelling is responsible for about 50% of the total supercomputing time worldwide (and it is not declining); about 2/3 of this time are spent on QM models and 1/3 is spend on empirical models. We are able to develop MLIPs that are nearly as accurate as the QM models, while 1000 to 10000 times more efficient – this means that we enable solving problems that could otherwise be solved only on computers that will be available 15 to 20 years from now.

 

Moment Tensor Potentials

Moment Tensor Potentials (MTPs) are a family of local MLIPs adopting a linear regression model with a very smartly chosen basis functions. These functions rely on describing neighborhoods of atoms with tensors of inertia (of the system of neighboring atoms). These functions are invariant with respect to all Euclidean transformations (rotations, reflection and translation) and permutation of atoms of the same chemical type. MTPs are able to approximate the behavior of any QM model (at least theoretically) by systematically increasing the number of parameters.  The performance of MTPs is much higher than that of the density functional theory (or DFT – this is the most popular QM model). Moreover, their computational complexity scales linearly with the number of atoms, whereas DFT has the complexity of around O(n³).

Training of MLIPs

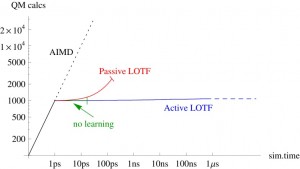
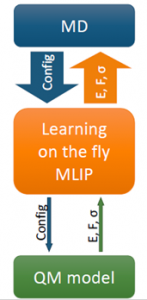
All MLIPs have a number of a priori unknown parameters found by requiring that the key quantities (e.g., the total energy, forces on atoms, stresses) are close to their QM counterparts on the training set. The training set can be constructed by active learning that allows training a MLIP on the fly. This scenario is of high practical importance, for example, in the context of a long molecular dynamics, where MLIP is employed for calculating the forces and from time to time requests QM data for fitting.

Comparison of ab initio molecular dynamics (AIMD) with no learning, passive learning on the fly (LOTF) and active LOTF. Passive learning on the fly have have limited reliability on this test case, while active LOTF is perfectly reliable.

Applications of MLIP

We have a number of research projects and applications of atomistic modeling for which MLIPs are successfully applied. The number of such projects rapidly grows. Among applications are: crystal structure prediction, finding of stable phases of alloys, automated alloy phase diagrams, estimating atomization energies of molecules, point defects diffusion, etc.

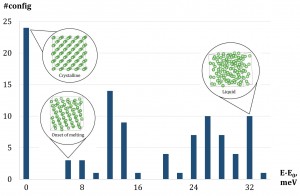
An illustration of congurations selected into the training set by active learning. The X-axis is the range of energies per atom of congurations after relaxation. The Y-axis is the number of congurations within a certain energy range. The training set features 24 crystalline congurations and 76 fully or partly liquid.