Atomistic-to-Continuum Coupling

Consider a microcrack in an infinite lattice stretched in the y direction (Figure 1). The easiest way to compute the displacements of atoms is by a direct atomistic simulation, here the microcrack is enclosed in a finite region and stretching is applied to the boundaries of that region. For the computation to be accurate, a large region is required, otherwise the displacement cannot be accurately resolved: notice that in Figure 1 the displacements at the boundary of a 10×10 square are quite large. This typically leads to a prohibitively large number of atomistic degrees of freedom (DoF) required to reach a desired accuracy. Indeed, as Figure 3 suggests, few hundred thousands of DoF are needed to reach the accuracy of 10^-2. Nevertheless, except in a small neighborhood around the microcrack, the atoms experience a smooth (elastic) deformation field which leads to the idea of applying continuum elasticity models far from the defect.

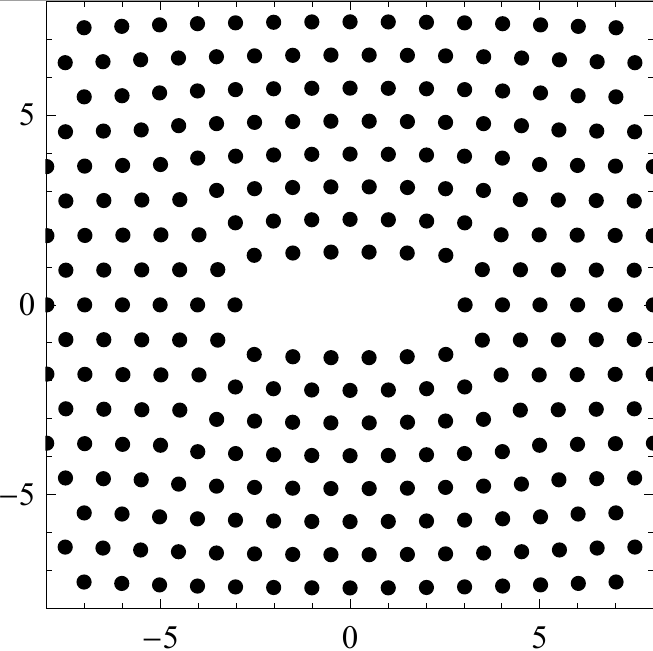
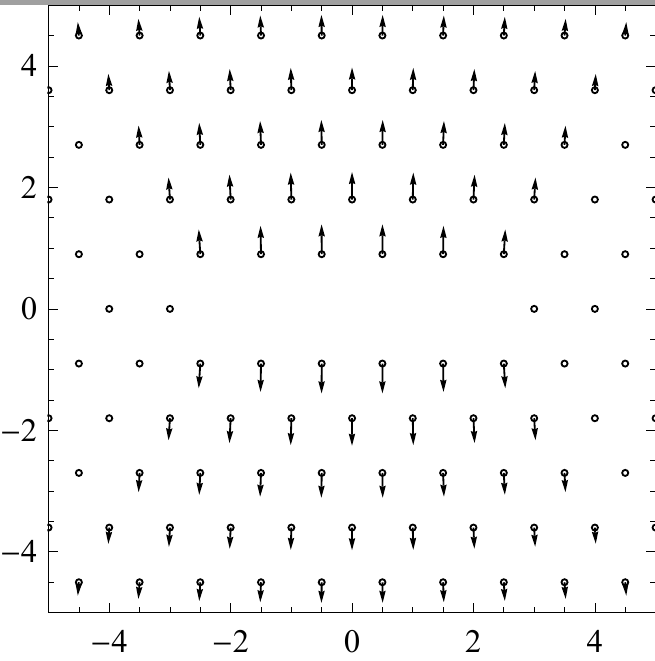
Figure 1: A microcrack defect. Although the missing atoms affect only atoms nearby through interatomic forces, the elastic displacement field is long-range.

The approach of atomistic-to-continuum (AtC) coupling, i.e., coupling atomistic and continuum models, has been widely used in materials science and engineering for two decades. It consists in surrounding the atomistic defect with a mesh (see Figure 2) and using the P1 (i.e., piecewise linear) finite elements discretization of a continuum elastic energy. One of the first systematic methods of AtC coupling was the (energy-based) quasicontinuum method (QCE). It was discovered, however, that it is not trivial to define the energy near the interface (since the nonlocal energy that depends on the distances between atoms is coupled to a local energy that depends only on the deformation gradient in the respective element). Indeed, QCE (as well as many other similar methods) exhibits uncontrollable errors near the interfaces that cannot be further reduced (see Figure 3). Such errors are related to lack of consistency, understood in a simplest form as the failure of the patch test: zero displacement is an equilibrium of both atomistic and continuum energies, yet it generates effectively nonzero forces (called ghost forces) in the coupled system.

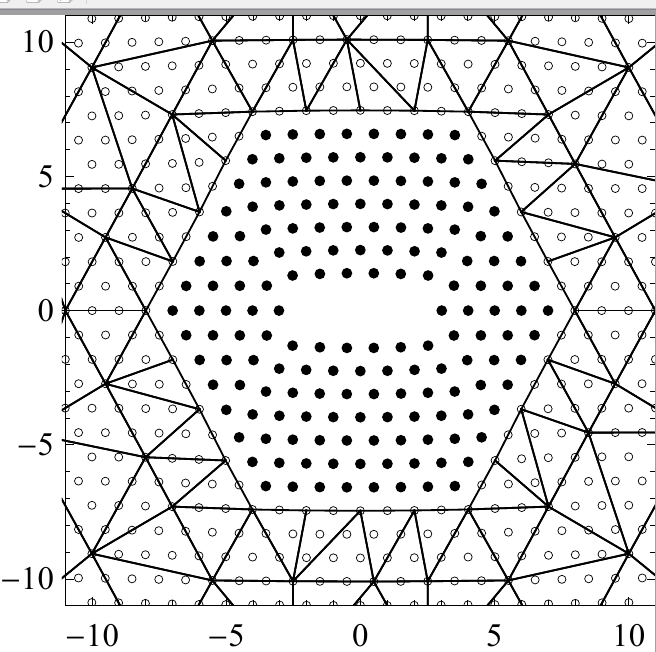
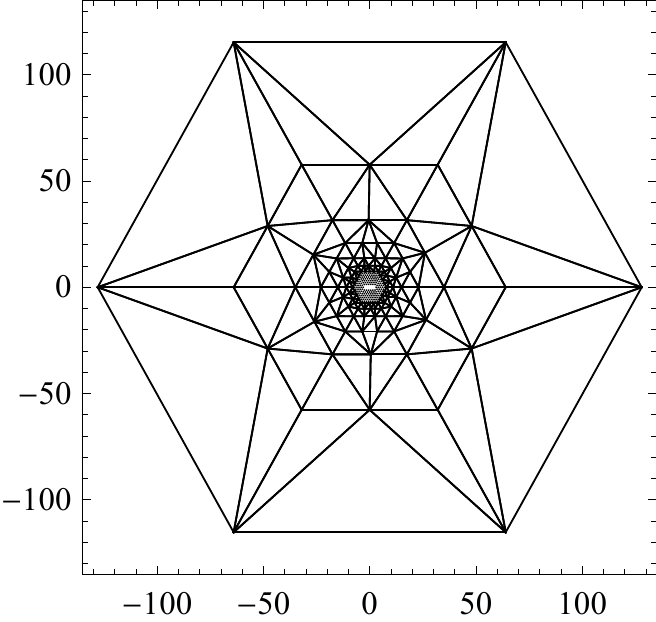
Figure 2: Geometry of the AtC coupling. Full atomistic resolution is preserved near the defect, whereas a finite element mesh discretization is used far from the defect. This allows the resolution of the long-range elastic fields.

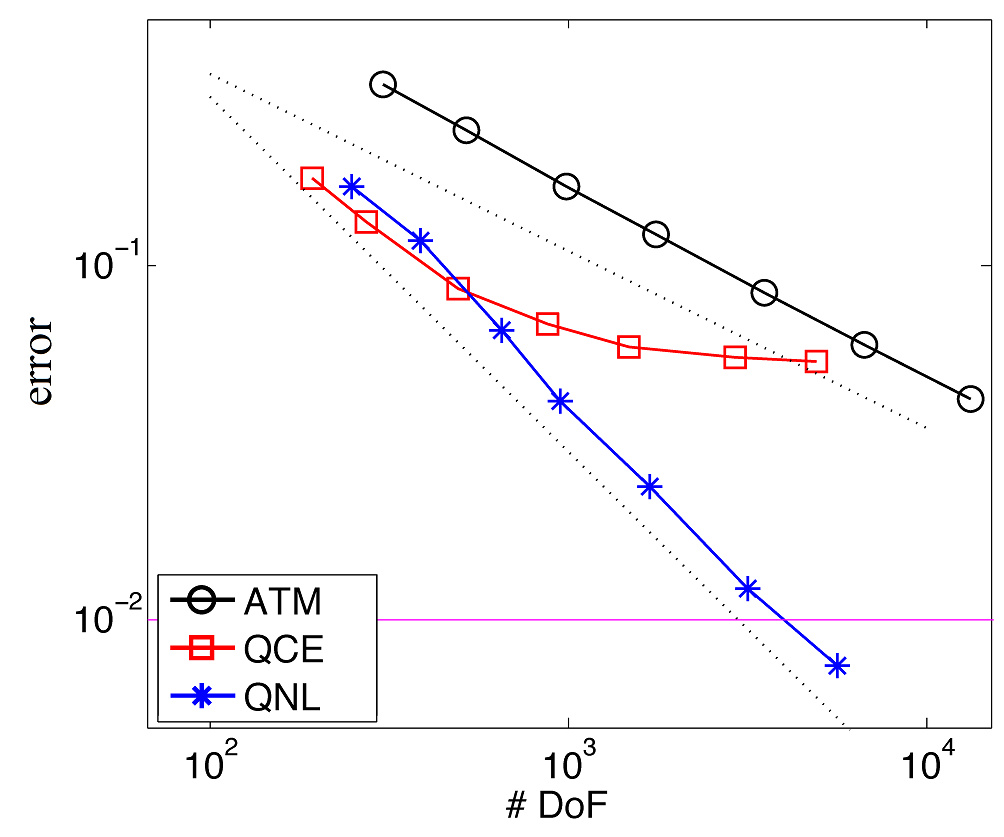
Figure 3: Energy norm errors of atomistic simulation. It takes few hundred thousand DoF to reach the accuracy of 10^-2 for a purely atomistic simulation, the QCE method never reaches it, and a consistent method (denoted as QNL) does it with few thousand DoF.

The most common solution is a so-called force-based coupling, where the coupled system does not have an energy, but instead we mix atomistic and continuum forces on the respective degrees of freedom. The force-based coupling indeed gets rid of uncontrollable interfacial errors, but its stability is not well understood and it cannot be used directly in some applications such as free energy sampling.

Blending is another practical idea that can be applied to increase accuracy and stability of both energy-based and force-based methods. It consists in a gradual transition from atomistic energy/forces to the continuum ones.

Finally, a sharp-interface consistent coupling attempts to completely eliminate the interface errors by tweaking the interfacial energy.

Refereed Articles

[12]	Analysis of an optimization-based atomistic-to-continuum coupling method for point defects (D. Olson, A. V. Shapeev, P. Bochev, M. Luskin), ESAIM: Mathematical Modelling and Numerical Analysis, volume 50, 2016. [bibtex] [doi] [arXiv]
[11]	Analysis of Boundary Conditions for Crystal Defect Atomistic Simulations (V. Ehrlacher, C. Ortner, A.V. Shapeev), volume 222, 2016. [bibtex] [doi] [arXiv]
[10]	An optimization based coupling method for multiscale problems (A. Abdulle, A. Shapeev O. Jecker), Multiscale Model. Simul., Society for Industrial and Applied Mathematics, volume 14, 2016. [bibtex] [pdf] [doi]
[9]	Theory-based Benchmarking of the Blended Force-Based Quasicontinuum Method (Xingjie Li, Mitchell Luskin, Christoph Ortner, Alexander V. Shapeev), Computer Methods in Applied Mechanics and Engineering, volume 268, 2014. [bibtex] [pdf] [doi] [arXiv]
[8]	(In-)Stability and Stabilisation of QNL-Type Atomistic-to-Continuum Coupling Methods (C. Ortner, A.V. Shapeev, L. Zhang), Multiscale Model. Simul., volume 12, 2014. [bibtex] [pdf] [doi] [arXiv]
[7]	An optimization-based atomistic-to-continuum coupling method (D. Olson, P. Bochev, M. Luskin, A. V. Shapeev), SIAM Journal on Numerical Analysis, Society for Industrial and Applied Mathematics, volume 52, 2014. [bibtex] [arXiv]
[6]	Analysis of an energy-based atomistic/continuum approximation of a vacancy in the 2D triangular lattice (C. Ortner, A. V. Shapeev), Math. Comp., volume 82, 2013. [bibtex] [doi] [arXiv]
[5]	A Priori and A Posteriori $W^1,infty$ Error Analysis of a QC Method for Complex Lattices (A. Abdulle, P. Lin, A. Shapeev), SIAM J. Numer. Anal., volume 51, 2013. [bibtex] [doi] [arXiv]
[4]	Consistent Energy-based Atomistic/Continuum Coupling for Two-body Potentials in Three Dimensions (A. V. Shapeev), SIAM J. Sci. Comput., volume 34, 2012. [bibtex] [doi] [arXiv]
[3]	The Spectrum of the Force-Based Quasicontinuum Operator for a Homogeneous Periodic Chain (M. Dobson, C. Ortner, A. V. Shapeev), Multiscale Model. Simul., volume 10, 2012. [bibtex] [doi] [arXiv]
[2]	Numerical Methods for Multilattices (A. Abdulle, P. Lin, A. V. Shapeev), Multiscale Model. Simul., volume 10, 2012. [bibtex] [doi] [arXiv]
[1]	Consistent Energy-Based Atomistic/Continuum Coupling for Two-Body Potentials in One and Two Dimensions (A. V. Shapeev), Multiscale Model. Simul., volume 9, 2011. [bibtex] [doi] [arXiv]