Advanced Quantization Methods
Abstract
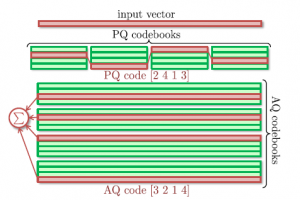
Additive quantization
We introduce a new compression scheme for high-dimensional vectors that approximates the vectors using sums of M codewords coming from M different codebooks. We show that the proposed scheme permits efficient distance and scalar product computations between compressed and uncompressed vectors. We further suggest vector encoding and codebook learning algorithms that can minimize the coding error within the proposed scheme. In the experiments, we demonstrate that the proposed compression can be used instead of or together with product quantization. Compared to product quantization and its optimized versions, the proposed compression approach leads to lower coding approximation errors, higher accuracy of approximate nearest neighbor search in the datasets of visual descriptors, and lower image classification error, whenever the classifiers are learned on or applied to compressed vectors.
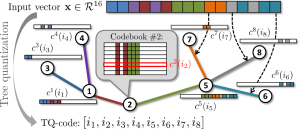
Tree quantization
We propose a new vector encoding scheme (tree quantization) that obtains lossy compact codes for high-dimensional vectors via tree-based dynamic programming. Similarly to several previous schemes such as product quantization, these codes correspond to codeword numbers within multiple codebooks. We propose an integer programming-based optimization that jointly recovers the coding tree structure and the codebooks by minimizing the compression error on a training dataset. In the experiments with diverse visual descriptors (SIFT, neural codes, Fisher vectors), tree quantization is shown to combine fast encoding and state-of-the-art accuracy in terms of the compression error, the retrieval performance, and the image classification error.
Data
VLAD-500K dataset (from the AQ paper) download
Deep1M dataset (from the TQ paper) download
Data is stored in .*vecs format described here
Source code
AQ implementation link
TQ implementation – Coming soon